
FLUID MECHANICS
Common terms used in Fluid Mechanics
- Definition of Fluids
Fluids may be defined as those substance, which has the ability to flow. It has no definite shape. But it conforms the shape of the containing vessel. When a small shear force is applied on it, it undergoes the deformation as long as the force continues to be applied. Both liquids and gases are called fluids. Fluids can be divided in to Ideal Fluids and real fluids.
| Quantity | S.I system Symbol (Unit) |
Metric System Gravitationl Units (Symbol) |
|---|---|---|
| Velocity | m/s(metre per second) | m/sec (metre per second) |
| Angular Velocity | rad/s(radians per second) | rad/sec (radians per second) |
| Acceleration | m/s2(metre per second square) | m/sec2(metre per second square) |
| Angular Acceleration | rad/s2(radians per second square) | rad/sec2(radians per second square |
| Mass density | kg/m3 (Kilogram per cubic metre) | msl/m3(metric slug per cubic metre) |
| Frequency | Hz ( Hertz) | 1/sec |
| Pressure | N/m2 ( Newtons per square metre) | kg(f)/m2 ( Kilogram(f) per square metre) |
| Elastic Modulus | N/m2 ( Newtons per square metre) | kg(f)/m2 ( Kilogram(f) per square metre) |
| Stress | N/m2 ( Newtons per square metre) | kg(f)/m2 ( Kilogram(f) per square metre) |
| Weight Density | N/m3 ( Newtons per cubic metre) | kg(f)/m3 ( Kilogram(f) per cubic metre) |
| Specific Weight | N/m3 (Newtons per cubic metre) | kg(f)/m3 ( Kilogram(f) per cubic metre) |
| Dynamic Viscosity | N-s/m2 or Pa-s (Newton second per square metre (Pascal Second) | kg(f)-sec/m2 ( Kilogram(f)-second per square metre) |
| Kinematic Viscosity | m2/s (Square metre per sec) | m2/sec (Square metre per sec) |
| Work, Energy, Torque | J( joule) | Kg(f)-m( Kilogram (f) metre) |
| Power | W (watt) | Kg(f)-m/Sec (( Kilogram (f) metre per second) |
| Quantity of Heat | J ( joule) | Kcal ( Kilo-calorie) |
| Momentum | kg-m/s( Kilogram metre per second) | msl-m/sec( metric slug-metre per second) |
| Surface Tension | N-m(Newton per metre) | Kg(f)/m ( Kilogram force per metre) |
| Gas Constant | J/(Kg.K)Joule per Kilogram Kelvin | Kg(f)-m/msl 0C (Kilogram (f) metre per metric slug egree centigrade ( abs) |
Conversions
Temperature
Degree C (abs) TO Degree K
Degree F (abs) TO (0R)
0 R TO Kelvin (K)
TK = 0C + 273.15 , 0R = F + 459.67, 0R = 1.8 x K
Gas Constant
R = 8.3144598 J/mol-K
R = 0.08206 L- atm. /mol-K
R = 8.3144598 m3Pa/mol-K
R = 1.987 Cal/ mol-k
R = 62.36 L-Torr/ mol-K
Volume
1 cm3 = 0.061 in 2
1 m3 = 35.315 ft 3
1 litre = 0.0353 ft 3
1 litre = 0.220 imp . gal
1 litre = 0.264 US Gal
1 US gal = 3.785 litre
1 imp gal = 4.546 litres
1 ft3 = 28.3 litres
1 ft3 = 0.0283 m3
1 in3 = 16.387 cm3
Mass
1 lb (m) = 0.453 6 kg(m)
1 lb (m) = 0.03108 slug
1 lb (f) = 0.4536 kg(f)
1 kg(m) = 2.205 lb(m)
1 kg (m) = 0.0685 slug
Mass Density
1 msl/m3 = 0.019 slug/ft3
1 gm/cc = 1 kg(m)/litre
1 lb(m)/ft3 = 0.01602 gm/cc
Weight Density
1 kg (f)/cm2 = 14.22 lb(f)/ft3
1 kg(f)/m3 = 9.81 N/m3
1 N/m3 = 0.1020 kg(f)/m
- Mass Density
It can be defined as mass per unit volume of the substance and its unit is kg/m3
- Specific Weight
It is the Weight of the substance per unit volume and it is denoted by the Greek letter,
( gamma).
- Specific Volume
Specific volume of a substance is reciprocal of the density ,ie the volume occupied in cubic m per kg of the substance.
- Specific Gravity
Specific gravity of a substance refers to the ratio of density of the substance with reference to the density of pure water. It is also referred as relative density.
- Perfect Gas
A perfect gas is the gas which obeys the ideal gas laws, which connects the pressure , the space occupied the number of molecules and the absolute temperature of the gas ( Which obeys the oerfect gas equation Pv = nRT.)
- Viscosity
Viscosity is that property of the fluid which restricts the shear stress between two adjacent layers in fluid flow. A liquid is called a Newtonian Fluid, when the shear stress is linear with the angular deformation.
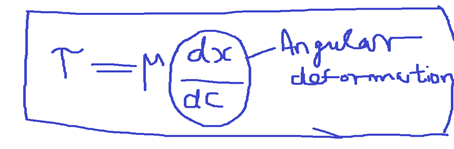
The coefficient is called coefficient of viscosity or Dynamic viscosity.
If We divide dynamic viscosity by density, We will get kinematic viscosity.
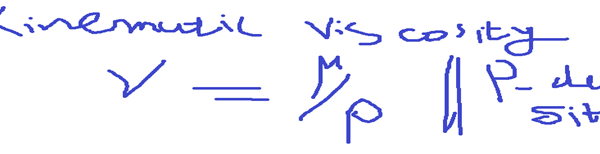
- Vapour Pressure
The vapor pressure is the equilibrium pressure exerted by the vopor over its liquid or solid phase in a closed container.
10.Surface Tension and Capillary action
The property of the surface of the liquid that allows it to resist an external force. This happens due to the cohesive nature of the molecules. Some physical examples of surface tension forces are, the spherical shape of the liquid drops, spherical shape of soap bubbles, small insects standing on the surface of liquids etc. It is the tendency of the liquid surfaces at rest to shrink to reduce its surface area to the possible extent.
The ascending action of a liquid through a narrow tube naturally placed on the liquid surface due to the adhesive and cohesive forces interaction of the liquid and surface molecules.
When adhesive forces are more predominant than cohesive forces, capillary action occurs.
11.Shear Stress
Shear stress is the deforming forces acting per unit area of the deformed object due to an external force acting on a body causing deformation.
12.Kinematic Viscocity
Kinematic viscosity is the ration of dynamic viscosity to the density of the fluid.
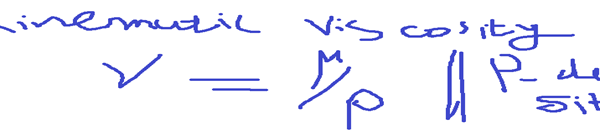
- Dynamic Viscocity
Dynamic viscosity, μ called the proportional constant of the relation between Shear stress and angular deformation.

- Compressibility of Liquid
It is the change in fluid volume due to change per unit change in pressure. A liquid normally does not exhibit any yield stress when pressure is applied on it.
- Fluid Pressure
Fluid pressure, is defined as the force exerted per unit area of the fluid , perpendicular the area of a fluid or on the walls of a closed container. Its unit is N/m2 (Pascal).
- Pascal’s law
The pressure at any point in a fluid at rest has equal magnitude in all directions. When a certain pressure is applied at any point in a fluid at rest, it is equally transmitted to every other point equally in all directions. This is called Pascal’s Law.
- Boyle’s Law
Boyle’s Law states that, at constant temperature, the volume of a gas varies inversely to the pressure.
Volume (v) = constant / Pressure (P) , at constant temperature.
- Manometres
Manometres are pressure measuring device,adopted for the measurement of pressure in a fluid. It uses the same liquid column for balancing the pressure due to the column of a liquid or uses a different liquid column for balancing. The manometers may be classified as simple or differential manometers.
- Buoyancy and Centre of Buoyancy
When a body is immersed in a fluid (It can be partial immersion also), an upward force will act on the body, trying to lift the body against the forces of gravity.
This phenomenon is called Buoyancy. The force in such conditions, trying to up lift the body is called Buoyant Forces. These buoyant forces act on a point on the body called, Centre of Buoyancy.
- Meteacentre and Metacentric height
A metacentre is defined as a point on a body in stable equilibrium, about which it starts to oscillate, when tilted by an angular displacement.
Metacentric height is the distance between the metacentr of a floating body and its centre of gravity.
As metacentric height increases, the stability of the floating body increases but period of oscillation decreases, which produces large vibration in the case of ships, which causes discomfort to the passengers on board.
- Stability of a wholly submerged body
A submerged body is said to be stable, when the center of gravity (C.G) of the body lies below the center of buoyancy of the displaced liquid. A submerged body is said to be in neutral equilibrium for all positions, if its centers of gravity and buoyancy coincides.
22.Time Period of Transverse Oscillation of a Floating Body
A floating body in a state of equilibrium may be set to a state of oscillation, when it is suspended at the metacenter M of the body. This can happen when an overturning couple by which a floating body is tilted, is removed suddenly.
- Steady Flow and Unsteady Flow
A flow is said to be steady, if its parameters do not change w.r.t time.
A flow is said to be unsteady, if one or more of the flow parameters changes w.r.t time.
24.Uniform Flow and Non –uniform flow
When the velocity of flow of fluid does not change both in magnitude and direction point to point during any given instant of time, then the flow is said to be in uniform flow.
If the velocity of flow changes from point to point in the flowing fluid, then the flow is said to be non-uniform.
- One dimensional ,two dimensional, three dimensional flow
When fluid flow occurs, definitely the various characters of the flowing fluid may vary( functions of space and time).
For example, say velocity of a flowing fluid will vary, the following representation of velocity, clearly distinguishes between 1,2 and 3 dimensional flow.
Type of flow Unsteady Steady
One dimensional V = f( x,t) V = f(x)
Two dimensional V = f(x,y,t) V = f(x,y)
Three dimensional V = f (x,y,z,t) V = f(x,y,z)
- Rotational Flow and Irrotational Flow
When the fluid is flowing , and one molecule is rotating along its own axis ,then it is called rotational flow.
When fluid molecules travel from one position to another, and there will not be any rotational motion, then that type of flow is called irrational flow.
27.Laminar Flow
A flow is said to be laminar, when the various fluid particles moves in layers and one fluid layer slides smoothely over the adjacent fluid layers .Viscosity plays an important role in laminar flow. In general, flow of all highly viscous fluids can be treated as laminar flow.
- Turbulent Flow
When the fluid particle moves in a flow, in an entirely haphazard or disorderly manner, then the flow is said to be turbulent. The rapid and continuous mixing of the momentum transfer occurs in such flow patterns and which will result in eddy and vortices formation of different sizes, which travels long distances in the flow.
- Streamline
Streamlines are lines tangential to the velocity vectors. For steady flow stream lines do not change with time. But for unsteady flow, streamlines change with time.
30.Stream-tube
A stream-tube is a tube imagined to be formed by a group of stream lines , passing through a small closed curve ,which may or may not be circular.

31.Path –line
Path lines trace the path of one fluid element in space.
For steady flow, streamlines, streak line and path lines are identical.
32.Streak-line
Streak-lines are a set of fluid elements that pass through a fixed point in space
33.Principle of Conservation of Mass, Energy and Momentum
The principle of conservation of mass states that mass can neither be created nor be destroyed. The continuity equation is derived based on this.
The principle of conservation of energy sates that, energy can neither be created nor be destroyed.
The principle of conservation of momentum states that, the impulse of the resultant force; product of force and time increment during which acts, is equal to the change in momentum of the body.
- Continuity Equation
The general continuity equation is,
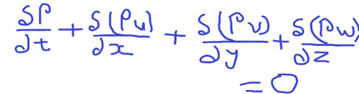
The terms in the equation is as shown below.
p-density
t -time
u- Velocity component in x-direction
v – Velocity component in y-direction
w – Velocity components in z-direction
Note: The above equation is valid for steady/unsteady flow, viscous or frictionless flow, compressible or incompressible flow.
Vector notation in terms of the velocity vector v:
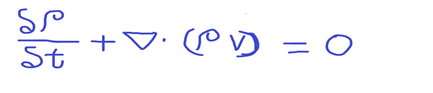
∇ – del operator or vector gradient operator
p – density
v – velocity
Where Del operator , ∇ is given as

- Circulation and Vorticity
The flow along a closed curve is called circulation. (The flow in Eddies and vortices ).The mathematical concept of circulation is the line integral,taken completely around a closed curve of the tangential component of the velocity vector.
Fig. above is the circulation around a closed curve.
The definition vorticity is ,
Vorticity – Circulation / Area.
Vorticity ( zeta) , = Circulation / Area
Vorticity is a vector quantity.
If the vorticity, is zero in all regions, then the flow in that region is said to be irrotational . On the other hand the flow in regions, where vorticity is other than zero is said to be rotational.
The physical meaning of circulation is that, the amount of force that pushes fluid along a closed boundary or path is called circulation.
Vorticity is the tendency of the element of fluid to spin. Vorticity can be related to the amount of circulation in a fluid.
Rotational flow has vorticity, while irrotational flow has no vorticity .
36.Velocity Potential
The velocity potential,a scalar function of space and time ,which is defined as the negative derivative of it w.r.t any direction gives the velocity of the fluid in that direction.

37.Stream Function
The stream function is defined as the scalar function of space and time such that its partial derivative w.r.t any direction, gives that component of velocity right angles to this direction.
38.Streamlines,Equipotential lines, and Flow Net
Streamlines are lines tangential to the velocity vectors. For steady flow stream lines do not change with time. But for unsteady flow, streamlines change with time.
Equipotential lines are those lines along which the velocity potential is constant. The slop of equipotential lines, dy/dx = -u/v
- Charles Law
The volume of a given mass of gas , varies directly with its absolute temperature, when the pressure of the gas is kept constant.
- Ideal Gas Law
It states that, the product of pressure and volume of 1 gram molecule of an ideal gas is equal to the product of the absolute temperature of the gas and the universal gas constant ( R) .
ie ; pv = nRT
p – pressure
v – volume
n – number of moles
R – Universal Gas Constant
T – Absolute Temperature of the gas.
41 Avogadrow’s Law
At same Temperature and pressures, equal volume of different gases contains same number of molecules.
42 Gay Lussac’s Law
It states the pressure of a gas varies directly with its absolute temperature, when the mass and the volume is kept constant.
(P1/T1) = (P2/T2).

